Por Cesar F. Caiafa y Sergio E. Lew
Muy probablemente, el lector haya descubierto el término Inteligencia Artificial (IA) a través de la literatura fantástica o producciones cinematográficas que, frecuentemente, aluden a un futuro dominado por la tecnología y plagado de robots humanoides. Sin duda, esas obras de ciencia ficción estuvieron inspiradas en discusiones científicas iniciadas a partir de mediados del siglo XX con la aparición de las primeras computadoras y con la idea de que éstas pudieran imitar, y hasta superar, las habilidades intelectuales de los humanos. No es casual que Isaac Asimov, autor del libro de ciencia ficción pionero en IA publicado en 1950: “Yo, Robot” (Asimov, 2001), fuera profesor de la Universidad de Boston, doctorado en Química, cuyo desempeño en la academia le permitió estar al tanto de los avances en las por entonces florecientes ciencias de la computación.
Si bien en el pasado reciente la IA pertenecía casi exclusivamente al mundo de la ciencia ficción o era materia de estudio de un puñado de científicos, durante los últimos años hemos comenzado a familiarizarnos con este término que ya forma parte de nuestra vida cada día. Nuestros teléfonos celulares están dotados de IA, nos sugieren itinerarios óptimos, nos recomiendan artículos para comprar y nos identifican en una fotografía tomada por un contacto en una red social, entre otras acciones cotidianas. La IA, ha dejado de ser una idea futurística para formar parte de nuestras vidas, además de tener un rol relevante en el desarrollo de la ciencia moderna. Nos permite descubrir inteligentemente nuevas drogas para tratamientos de enfermedades, ayuda a los médicos a diagnosticar enfermedades a partir de imágenes, asiste a los astrónomos en el análisis de grandes volúmenes de datos para validar nuevas teorías científicas, entre otras aplicaciones a la ciencia. Pero ¿de qué hablamos exactamente cuando nos referimos a la IA? En este breve artículo, se cuenta brevemente la historia de esta tecnología con una introducción a sus principios fundamentales y utilidades.
Los orígenes de la IA
Desde ya hace mucho tiempo, se ha utilizado el método científico, basado en la evidencia objetiva a partir de la medición de variables y la aplicación de leyes de las matemáticas, para diseñar procesos automáticos ejecutados por máquinas que pudieran reemplazar o mejorar las capacidades de los humanos en lo que refiere a la toma de decisión inteligente. Así, podemos definir la IA como la capacidad de las máquinas de tomar decisiones óptimas en algún sentido, por ejemplo, minimizando la probabilidad de cometer un error en cada decisión. Además, se busca diseñar máquinas que puedan “aprender” a partir de ejemplos suministrados o mediciones del entorno, tal como lo hacemos los humanos y otras especies animales que hemos desarrollado la capacidad de tomar decisiones basadas en la experiencia. Desde que somos niños, exploramos el mundo que nos rodea y aprendemos de nuestra interacción con el ambiente. Por ejemplo, cuando un niño que se quema al tocar una estufa, se genera un mecanismo por el cual muy probablemente, la próxima vez que se encuentre ante la misma situación, evite tocarla.
Con la creación de las primeras computadoras en tiempos de la 2da Guerra Mundial, surgieron las ciencias de la computación. Los científicos comenzaron a idear algoritmos y a debatir acerca del significado filosófico de inteligencia y de las posibilidades de que las computadoras fueran inteligentes. Las herramientas matemáticas que facilitaron el desarrollo de una teoría de la IA son la estadística y la teoría de las probabilidades ya que han permitido modelar la realidad a través de variables aleatorias y secuencias de eventos que actúan sobre ellas.
Sin embargo, antes de la aparición de las computadoras, ya se habían propuesto métodos matemáticos, precursores de la IA, para la clasificación de muestras experimentales. R. A. Fisher, quien es considerado uno de los padres de la estadística moderna (Fig. 1a), propuso en 1936 un método para la clasificación de muestras pertenecientes a dos posibles clases de flores (Fisher, 1936). La formulación de Fisher estaba motivada por un problema práctico concreto al que se había enfrentado mientras trabajaba en una estación agrícola experimental: ¿Cómo desarrollar un método científico para clasificar muestras de flores a partir de la cuantificación de sus características? Más concretamente, Fisher tenía acceso a un conjunto de muestras de flores silvestres las cuales pueden pertenecer a dos clases posibles: iris setosa o iris versicolor, y de las cuales medía su morfología, por ejemplo, registrando el tamaño de sus pétalos y sépalos (Fig. 1b). Como las especies son morfológicamente diferentes, si graficamos los datos medidos, se obtienen dos nubes de puntos que pueden ser separados por una línea recta (ver puntos azules y rojos en la Fig. 1c-d).
El problema de Fisher plantea las siguientes preguntas: dado un conjunto de muestras, ¿Cómo definimos la línea que separa a los grupos de manera óptima? Por otro lado, supongamos que posteriormente, llega a nuestras manos una nueva muestra de la cual no conocemos a qué clase pertenece, ¿con qué clase la deberíamos asociar?, y ¿cuál es el error que podríamos cometer? El discriminante lineal de Fisher permite responder satisfactoriamente estas preguntas siendo la solución óptima para el caso en que las distribuciones de las clases son gaussianas y de igual varianza (Fisher, 1936). La solución propuesta por Fisher se ilustra en la Fig. 1d en contraposición a una solución no-óptima mostrada en la Fig. 1c.El problema abordado por Fisher es lo que hoy se conoce como un problema clásico de IA denominado aprendizaje supervisado. Se trata de “aprender” el clasificador óptimo identificando los parámetros que definen la recta que mejor separa las clases. El aprendizaje es “supervisado” porque tenemos a disposición un conjunto de muestras de las cuales conocemos la información de clases.
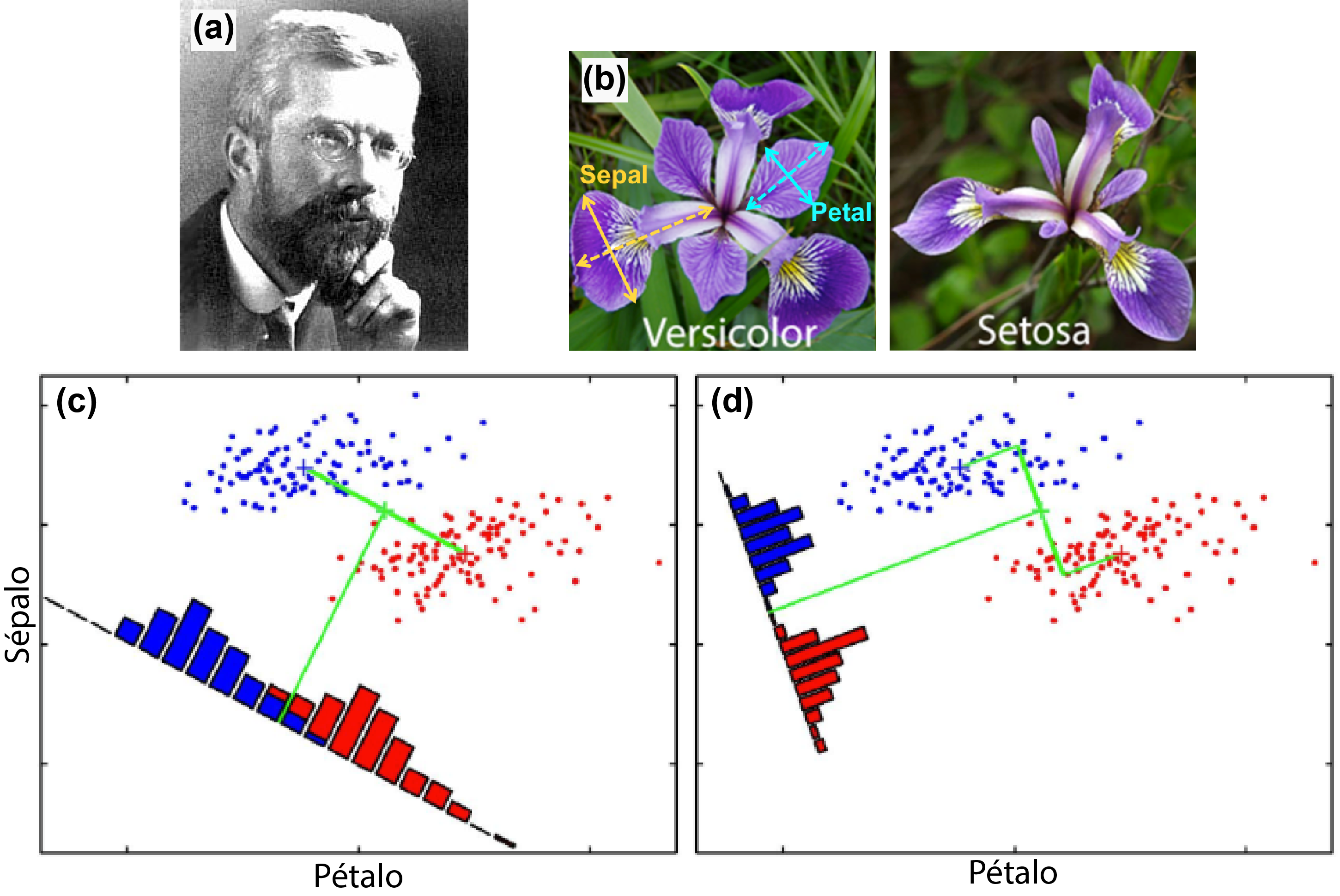
Figura 1: Discriminante lineal de Fisher (Fisher, 1936). (a) Ronald Aylmer Fisher (1890 – 1962). (b) Ejemplos de muestras de flores iris versicolor e iris setosa. (c) Clasificador no-óptimo obtenido como una línea perpendicular al segmento que une las medias de ambos grupos. (d) Clasificador lineal de Fisher (óptimo) (Fisher, 1936).
Simultáneamente al desarrollo de Fisher, también se comenzaban a desarrollar las primeras ideas que posibilitaron más tarde la aparición de las primeras computadoras. Alan Turing, considerado uno de los padres de las ciencias de la computación, publicó en 1936, quizás su artículo más influyente donde definía una máquina abstracta de cómputo, la Máquina de Turing, capaz de realizar cualquier cálculo a través de un programa (algoritmo). Este concepto, fue revolucionario en ese momento permitiendo el desarrollo de la computación moderna años más tarde.
La idea de poder desarrollar máquinas capaces de calcular y tomar decisiones dió lugar a interrogantes filosóficos, por ejemplo: ¿Puede una máquina pensar?, ¿Qué es la inteligencia? ¿Puede una máquina ser inteligente? ¿Puede una máquina tener conciencia? Matemáticos, filósofos y biólogos discutían en debates públicos confrontando sus ideas. Es famoso el debate público del que participó Turing titulado “Discusión sobre la mente y la computadora” el 27 de octubre de 1949, cuya transcripción puede encontrarse aquí (Turing, web).
Si bien se suele asumir el nacimiento de la IA en 1956 en una conferencia de verano en el Dartmouth College (Moor, 2006) donde se acuñó ese término por primera vez, la idea ya había sido trabajada y propuesta por Turing varios años antes. Por ejemplo, en 1947, en la sede de la Royal Astronomical Society de Londres, Turing habló de la inteligencia informática y declaró “Lo que queremos es una máquina que pueda aprender de la experiencia” (Copeland, 2004; Copeland, 2013). Además, en 1950 Turing publicó su famoso artículo “Computing Machinery and Intelligence”, donde abordaba la posibilidad de que las computadoras pudieran pensar (Turing, 1950).
Los años 50’s y 60’s: el perceptrón simple
Inspirados en la estructura y comportamiento fisiológico de la neurona, en 1943 el neurólogo W. McCulloch junto a W. Pitts propusieron su primer modelo matemático (McCulloch & Pitts, 1943). En este modelo, la neurona consta de varias entradas y una salida que se obtiene a través de una combinación lineal de las entradas usando coeficientes (pesos sinápticos) seguido por una operación no lineal conocida como función de activación (ver Fig. 2a).
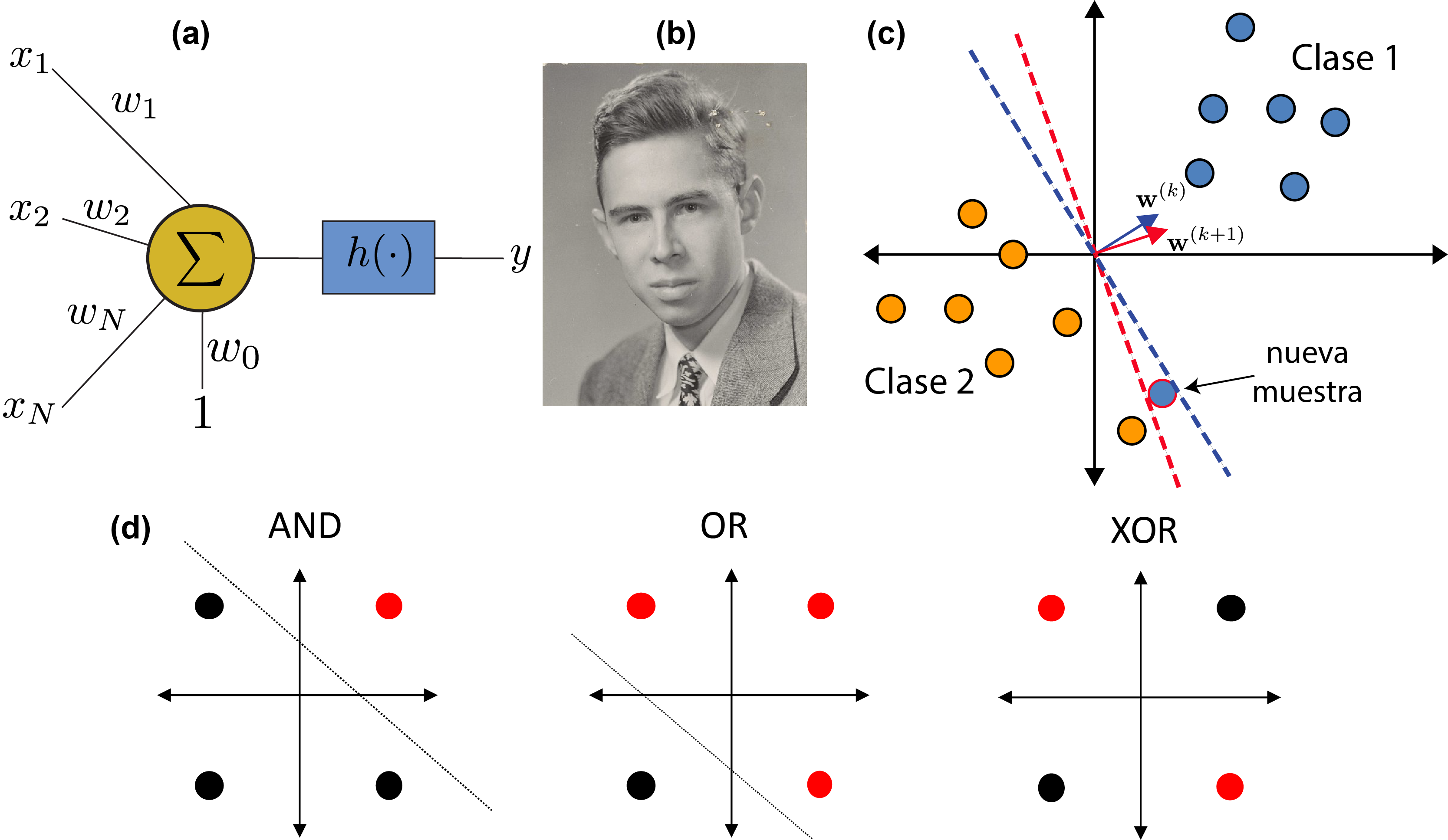
Figura 2: El Perceptrón simple (McCulloch & Pitts, 1943) (Rosenblatt, 1957). (a) Modelo matemático de una neurona. (b) Frank Rosenblatt (1928- 1971). (c) Dado un clasificador en la instancia k-ésima, al recibir una nueva muestra los pesos del clasificador son actualizados, dando lugar a un nuevo clasificador. (d) El perceptrón puede implementar las funciones lógicas AND y OR, pero falla con la función XOR porque ésta no es linealmente separable.
En 1957, F. Rosenblatt (Fig. 2b) le puso nombre al modelo neuronal de McCulloch-Pitts llamándolo Perceptrón y propuso un algoritmo iterativo (Fig. 2c) por el cual los pesos de la neurona se actualizan iterativamente de manera de converger al clasificador óptimo de las muestras suministradas (Rosenblatt, 1957). De esta manera, la neurona se “entrena” para discriminar entre dos clases linealmente separables. Es muy interesante destacar que este modelo coincide con el Discriminante de Fisher cuando la función de activación es la función signo y los datos responden a distribuciones gaussianas.
El algoritmo adaptativo de Rosenblatt motivó a los científicos al desarrollo de las redes neuronales artificiales interconectando varias neuronas que podían ser entrenadas para resolver problemas de clasificación. Sin embargo, en ese entonces aún no existían teorías que justificaran su eficacia. Más aún, en el año 1969, M. Minsky y S. Papert publicaron un libro en el que destruyeron al perceptrón simple a través de un sencillo ejemplo en el cual éste fallaba rotundamente. Estos autores demostraron que el perceptrón podía aprender funciones lógicas simples de tipo AND y OR, pero no podía hacerlo con la función lógica OR exclusiva (XOR) (ver Fig. 2d), lo cual sugería que el perceptrón no podía aprender funciones lógicas complejas, básicamente porque éstas no eran linealmente separables.
Los años 80’s: el auge de las redes neuronales artificiales
Las críticas de Minsky y colegas a finales de los años 1960’s frenaron el desarrollo de las redes neuronales artificiales por más de diez años. Increíblemente, el problema del perceptrón simple con la función XOR podía solucionarse sencillamente concatenando capas de neuronas como lo indicaron en 1986 Rumelhart, Hinton y Willams (Rumelhart et al, 1986). La explicación era muy sencilla y está ilustrada en la Fig. 3a-b, donde la primera capa contiene dos neuronas cuyas salidas operan como entradas de la única neurona de la segunda capa.
El artículo de Rumelhart, Hinton y Willams dió un tremendo impulso a las arquitecturas de redes multicapa que, si bien se conocían desde hacía varios años, hasta ese momento parecía no existir una metodología clara y práctica para poder entrenarlas. En ese artículo, los autores implementan eficientemente la técnica iterativa llamada backpropagation, que fuera propuesta anteriormente en (Kelley, 1960) y (Dreyfus, 1962). Esta técnica permite minimizar el error de clasificación iterativamente a través de actualizaciones de los pesos sinápticos de una capa por vez.
Por otro lado, las arquitecturas neuronales multicapa parecieran ser biológicamente plausibles. Por ejemplo, recientemente en experimentos de toma de decisión con monos, se encontró que en tareas lógicas simples, como la de diferenciar dos figuras, las neuronas del Núcleo Caudado responden aproximadamente 150 milisegundos antes que las neuronas de la corteza Prefrontal (Pasupathy & Miller, 2002), mientras que en tareas complejas que requieren de funciones lógicas linealmente no separables, los tiempos de procesamiento se incrementan. Esta actividad neuronal pone en evidencia la estructura multicapa que permite resolver estas reglas, con la corteza Inferotemporal como capa predecesora de la corteza Prefrontal (Freedman et. al, 2002). Además, el auge de estudios en Neurociencias y sus descubrimientos fueron fuentes de inspiración para la construcción de sistemas artificiales. A mediados de siglo XX, Hubel y Wiesel habían descubierto dos tipos de neuronas en la corteza visual primaria (V1) en gatos (Hubel, 1962). En el primer tipo (células simples), las neuronas se activaban con estímulos en forma de barras orientadas espacialmente. Las neuronas del segundo tipo (células complejas) recibían en sus entradas las salidas de las neuronas simples (ver Fig. 3c – izquierda). En 1980, K. Fukushima utilizó el principio de funcionamiento de la corteza visual descubierto por Hubel y Wiesel para diseñar el Neocognitron (Fukushima, 1980), una red neuronal que podía entrenarse para reconocer caracteres escritos a mano. Esta red fue la primera del tipo de lo que hoy se conocen como redes neuronales convolucionales. En estas redes, se entrenan pequeños filtros capaces de detectar patrones locales en imágenes como pueden ser barras con distinta orientación (ver Fig. 3c – derecha). En 1989, Yann Lecun propondría configuraciones de redes neuronales convolucionales con varias capas entrenadas con el método backpropagation con las cuales se pudieron alcanzar excelentes resultados en reconocimiento de caracteres manuscritos, incluso superando la performance humana.
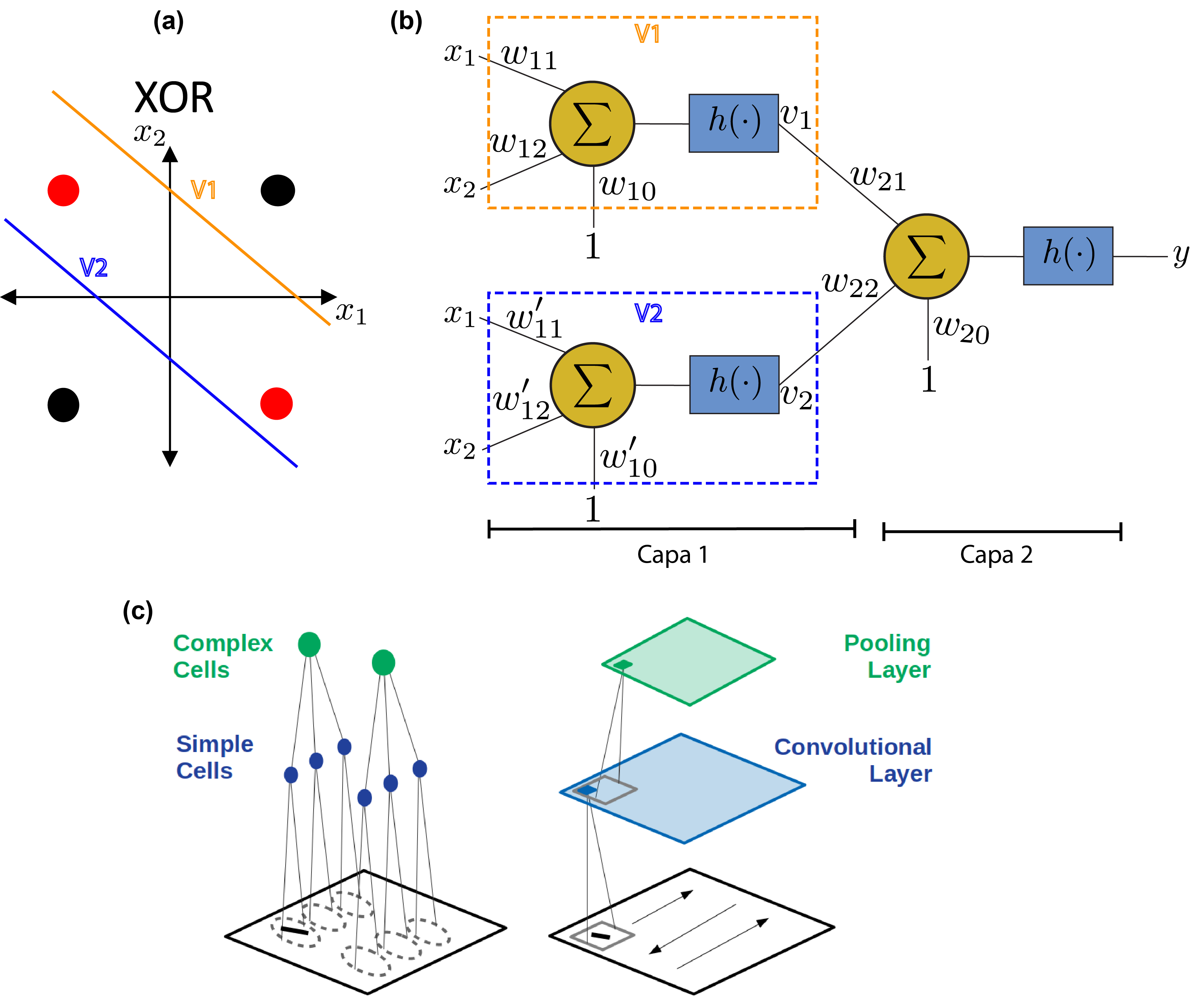
Figura 3: Redes neuronales artificiales multicapa. (a) implementación de la operación lógica XOR (OR exclusivo) a través de una red neuronal de 2 capas. (b) Red neuronal de dos capas. La primera capa contiene dos neuronas: V1 y V2, cada una de las cuales establece una separación lineal de los puntos como se indica en (a). La neurona de la última capa, combinada con las salidas de la primera capa, logra implementar efectivamente la función XOR. (c) Izquierda: Estructura de neuronas simples y complejas descubiertas por Hubel y Wiesel en la corteza visual de gatos (Hubel, 1962). Derecha: arquitectura de una red convolucional (figura extraída de (Lindsay, 2020))
Siglo XXI: Deep Learning, el triunfo de las redes neuronales artificiales en IA
Si bien las bases para la construcción de grandes redes multicapa se desarrollaron principalmente durante los años 1980’s y 1990’s, no fue hasta los años 2000’s en que efectivamente éstas pudieran ser implementadas eficientemente para resolver grandes desafíos prácticos, por ejemplo, en el reconocimiento de imágenes, el procesamiento del lenguaje natural, y otros. Este atraso en el desarrollo de la IA puede explicarse a partir de dos situaciones que se hicieron realidad recién en el siglo XXI: 1) La disponibilidad de grandes volúmenes de datos de entrenamiento a raíz de la proliferación de dispositivos digitales como los teléfonos celulares con cámaras fotográficas; y 2) La disponibilidad de hardware económico con gran poder de cálculo como es el caso de las primeras Unidades de Procesamiento Gráfico (GPU en inglés), que permitieron realizar en paralelo y de manera eficiente productos de convolución para detectar características propias de las imágenes.
A partir de este salto tecnológico, se pudieron construir las redes neuronales con decenas y hasta cientos capas de neuronas, conocidas como redes neuronales profundas y dando nacimiento al término Deep Learning para hacer referencia a este tipo de arquitecturas (Goodfellow et al, 2016). En el caso del análisis de imágenes naturales, las arquitecturas aprenden de los datos de entrenamiento ajustando los pesos sinápticos de las neuronas. Así, las primeras capas de neuronas aprenden a detectar patrones elementales locales, a nivel de píxeles de la imágen, mientras que las finales aprenden a identificar agrupaciones complejas de patrones elementales, como muestra el ejemplo de la Fig. 4a. De esta manera, una red neuronal profunda, logra capturar las características estructurales del conjunto de datos con el cual se la entrena. A diferencia de los métodos de detección de los años 80, donde los expertos definían cuáles eran las características que mejor definían a los datos, en las redes convolucionales profundas estas características se aprenden automáticamente durante el entrenamiento.
A partir de la implementación de redes neuronales en GPU’s, enormes fueron los desafíos y progresos en el área. Por ejemplo, Se desarrollaron modelos generativos para poder sintetizar artificialmente datos nuevos con las características esenciales del conjunto de datos de entrenamiento. Este tipo de redes se llaman Generative Adversarial Nets (GAN) y fueron introducidas en 2014 por Ian Goodfellow y colegas (Goodfellow et al., 2014). La Fig. 4b muestra algunas imágenes generadas artificialmente por una red neuronal entrenada con imágenes de rostros de celebridades (Karras et al, 2018). Notablemente, ninguna de estas personas existe realmente, los rostros fueron creados por una computadora. Similarmente, investigadores de Deep Mind, una compañía de IA adquirida por Google en 2014, lograron capturar estilos de pinturas de distintos autores famosos en una red neuronal y aplicarlo a cualquier imagen de entrada para generar una pintura nueva (ver Fig. 4c) (Gatys et al, 2015).
Las aplicaciones del Deep Learning van más allá del análisis y generación de imágenes. Una rama de la IA, conocida como aprendizaje por refuerzo (reinforcement learning) estudia sistemas que son capaces de aprender con la experiencia modificando su comportamiento dinámicamente a través de la realimentación con los resultados obtenidos. Por ejemplo, recientemente se ha demostrado que una máquina puede aprender a jugar Go, un juego estratégico más complejo que el ajedrez de origen asiático. En 2016, investigadores de DeepMind crearon AlphaGO, un sistema de IA que aprendió a jugar GO al ser entrenado con los mejores jugadores humanos de todo el mundo y logrando vencer al mejor jugador del mundo ese año (Silver et al, 2016). Un año más tarde, el mismo equipo de investigadores introdujeron AlphaZero que, a diferencia de su antecesor, fue entrenado jugando contra sí mismo alcanzando una performance aún mayor que su predecesor siendo, hasta el momento, imposible de vencer por un humano (Silver et al, 2017). Este fue uno de los sucesos más resonantes de la IA como fuera anunciado en la revista Science en 2018 (Silver et al, 2018).
Conclusiones
Más allá de las discusiones filosóficas sobre el significado de Inteligencia, los avances tecnológicos nos han demostrado que las máquinas pueden aprender a resolver, desde problemas sencillos hasta otros relativamente más complejos a través de métodos basados en matemática, principalmente utilizando teoría de probabilidades y estadística.
Así como los avances y descubrimientos en neurociencias sirvieron para inspirar sistemas de IA, debemos ser conscientes de que hay grandes diferencias entre las redes neuronales reales y las artificiales. Algunos científicos líderes en IA, como Yoshua Bengio de la Universidad de Montreal, están convencidos de que el desarrollo actual de la IA sólo permite resolver problemas cognitivos relativamente simples, como identificar patrones o conducir vehículos. Este tipo de tareas, son llevadas a cabo por los humanos de manera casi inconsciente una vez que han sido entrenados para ello.
El campo de la IA sigue en plena expansión mostrando resultados sorprendentes año tras año. Sin embargo, es notable que la mayoría de los algoritmos que muestran excelentes resultados experimentales no tienen un marco teórico que pueda explicar el porqué de ese comportamiento. Volviendo a la primer parte de este artículo, la IA actual, más allá de los logros alcanzados, sigue siendo una mera herramienta tecnológica, tal como lo fue la calculadora electrónica en la década del 70. Las redes neuronales pueden aprender por prueba y error, y con mucha exactitud, a resolver problemas lógico-matemáticos, muchas veces mejor que nosotros, los humanos, pero carecen de lo que tal vez originó aquellas fantasías de la ciencia ficción: la conciencia.

Figura 4: Deep Learning. (a) Arquitectura genérica de una red neuronal multicapa. En el caso de entrenarla con imágenes de rostros, la primera capa (input layer) captura patrones locales como bordes con distintas orientaciones. La segunda capa (hidden layer 1), captura agrupaciones de patrones locales formando por ejemplo los ojos, nariz, etc. La tercera capa (hidden layer 2), codifica los rostros completos combinando los patrones de las capas anteriores. (b) Ejemplos de imágenes de celebridades ficticias generadas por una red neuronal profunda GAN entrenada con rostros de celebridades reales (tomado de (Karras et al, 2018)). (c) Imagen original y sus versiones utilizando los estilos de distintos pintores (Van Gogh, Munch y Kandinsky). Estas imágenes fueron extraídas de (Gatys et al, 2015). (d) Portada de la revista Science, Vol. 362, Dic. 2018, sobre AlphaZero, un sistema de IA basado en Deep Reinforcement Learning que logra aprender a jugar Go, Ajedrez y Shogi sin interactuar con otros jugadores (Silver et al, 2018).
Bibliografía
- Asimov, I. (2001). Yo, Robot. Sudamericana.
- Copeland, B. (2004). The Essential Turing: Seminal Writings in Computing, Logic, Philosophy, Artificial Intelligence, and Artificial Life plus The Secrets of Enigma. Oxford University Press.
- Copeland, B. (2013). Alan Turing. El pionero de la era de la información. Turner.
- Dreyfus, S. (1962). The numerical solution of variational problems. Journal of Mathematical Analysis and Applications, 5(1), 30-45.
- Fisher, R. A. (1936). The use of multiple measurements in taxonomic problems. Annals of Eugenics, 179-188.
- Freedman, David J., et al. «A comparison of primate prefrontal and inferior temporal cortices during visual categorization.» Journal of Neuroscience 23.12 (2003): 5235-5246.
- Fukushima, K. (1980). Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biological Cybernetics, 36, 193-202.
- Gatys, L. A., Ecker, A. S., & Bethge, M. (2015). A Neural Algorithm of Artistic Style. CoRR.
- Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. New York: MIT Press.
- Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., . . . Bengio, Y. (2014). Generative Adversarial Nets. Advances in Neural Information Processing Systems 27.
- Hubel, D. H. (1962). Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. The Journal of physiology, 160(1), 106-154.
- Karras, T., Aila, T., Laine, S., & Lehtinen, J. (2018). Progressive Growing of GANs for Improved Quality, Stability and Variation. International Conference on Learning Representations.
- Kelley, H. (1960). Gradient theory of optimal flight paths. ARS Journal, 30(10), 947-954.
- Lindsay, G. (2020). Convolutional Neural Networks as a Model of the Visual System: Past, Present, and Future. Journal of Cognitive Neuroscience, 1-15.
- McCulloch, W., & Pitts, W. (1943). A logical calculus of the ideas immanent in nervous activity. Bulletin of Mathematical Biophysics, 5, 115-133.
- Moor, J. (2006). The Dartmouth College Artificial Intelligence Conference: The Next Fifty Years. AI Magazine, 27(4), 87-91.
- Pasupathy, Anitha, and Earl K. Miller. «Different time courses of learning-related activity in the prefrontal cortex and striatum.» Nature 433.7028 (2005): 873-876.
- Rosenblatt, F. (1957). The Perceptron–a perceiving and recognizing automaton. Cornell University.
- Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature, 323, 533-536.
- Silver, D., Huang, A., Maddison, J., Guez, A., Sifre, L., Van Den Driessche, G., . . . Kavukcuoglu. (2016). Mastering the game of Go with deep neural networks and tree search. Nature, 529, 484-489.
- Silver, D., Schrittwieser, J., Simonyan, K., Antonoglou, I., Huang, A., Guez, A., . . . Hassabis, D. (2017). Mastering the game of Go without human knowledge. Nature, 550, 354-359.
- Turing, A. (1950). Computing Machinery and Intelligence. Mind, LIX, 433-460.
- Turing, A. (web). Turing sources. Obtenido de https://www.turing.org.uk/sources/wmays1.html
- Warden, M. R., & Miller, E. K. (2007). The Representation of Multiple Objects in Prefrontal Neuronal Delay Activity. Cerebral Cortex, 17, 41-50.
Sobre los autores
Cesar F. Caiafa es Investigador Independiente CONICET del Instituto Argentino de Radioastronomía (IAR) y Profesor Adjunto del Departamento de Computación de la Facultad de Ingeniería, Universidad de Buenos Aires (FIUBA).
Sergio Lew es Investigador y Profesor Asociado en el Instituto de Ingeniería Biomédica (IIBM), Facultad de Ingeniería, Universidad de Buenos Aires (FIUBA).


